Matemática: Números Complejos

NÚMEROS COMPLEJOS

Información Para el Día a Día 

¿Qué es un Número?

Un numero es aquel Concepto matemático que expresa una cantidad con relación a la unidad de cómputo; resulta de contar los elementos que forman un conjunto, o en otro caso, puede ser un Signo gráfico o conjunto de signos gráficos que expresa o representa esa cantidad.

 En matemáticas un número puede representar una cantidad métrica o más generalmente un elemento de un sistema numérico o un número ordinal que representará una posición dentro de un orden de una serie determinada. Los números complejos son usados como una herramienta útil para resolver problemas algebraicos y que algebraica mente son un mero añadido a los números reales que a su vez ampliaron el concepto de número ordinal.

¿Existen Distintos Tipos de Números?
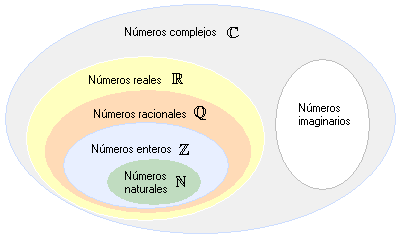
La respuesta es Sí, existen muchos tipos de números, entre los principales tenemos: 
Números Enteros

El conjunto de los números {...,-3 ,-2 ,-1 ,0,1,2,3,...}. se llama el conjunto de los enteros y se denota con la letra ℤ. Dentro de este conjunto hay subconjuntos diferentes. El conjunto {1,2,3,...} se llama el conjunto de los enteros positivos. El conjunto {...,-3 , -2 ,-1 } se llama el conjunto de los enteros negativos. Tenga en cuenta que el número 0, a pesar de que es un número entero, no es ni positivo ni negativo.

Números Naturales

El conjunto de los números naturales se denota con la letra ℕ y se define como el conjunto de los enteros positivos.
ℕ={1,2,3,...}.

Números Racionales

Los números racionales son el conjunto de números que pueden representarse como una fracción con dos números enteros. Es decir, los números racionales son aquellos números que pueden expresarse como mn, donde m y n son enteros y n≠0.
13,-54 ,30=301,0=0 5,0.25=14

Números Irracionales

Los números irracionales son números reales que no se puede expresar como una fracción de dos números enteros. Los números irracionales más comunes son π y las expresiones que contienen una raíz que no se pueden eliminar.

Ejemplo:

3,5, 23,-3 n 2

Números Reales

El conjunto de todos los números reales se denota por el símbolo ℝ y se puede considerar como el conjunto de todos los números que existen en la recta numérica. Esto incluye los números enteros, números racionales y números irracionales.

Números Complejos:

Los números complejos incluyen todas las raíces de los polinomios, a diferencia de los reales. Todo número complejo puede representarse como la suma de un número real y un número imaginario (que es un múltiplo real de la unidad imaginaria, que se indica con la letra I ), o en forma polar.

Los números complejos son la herramienta de trabajo del álgebra, análisis, así como de ramas de las matemáticas puras y aplicadas como variable compleja, ecuaciones diferenciales, aerodinámica y electromagnetismo entre otras de gran importancia. Además los números complejos se utilizan por doquier en matemáticas, en muchos campos de la física (notoriamente en la mecánica cuántica) y en ingeniería, especialmente en la electrónica y las telecomunicaciones, por su utilidad para representar las ondas electromagnéticas y la corriente eléctrica.

En matemáticas, estos números constituyen un cuerpo y, en general, se consideran como puntos del plano: el plano complejo. Este cuerpo contiene a los números reales y los imaginarios puros. Una propiedad importante que caracteriza a los números complejos es el teorema fundamental del álgebra, que afirma que cualquier ecuación algebraica de grado "x" tiene exactamente "x" numero de soluciones complejas. Los análogos del cálculo diferencial e integral con números complejos reciben el nombre de variable compleja o análisis complejo.

Realización de Operaciones con números complejos:

Suma

( a , b ) + ( c , b ) = ( a + c, b + d )

Producto Escalar

r ( a , b ) = ( ra , rb)

Multiplicación

( a , b ) . ( c , d ) = ( ac - bd , ad + bc )

Igualdad

( a , b ) - ( c , d ) = ( a - c , b - d )

Unidad imaginaria

Tomando en cuenta que ( a , 0 ) . ( 0 , 1 ) = ( 0, a ) , se define un número especial en matemáticas de gran importancia, el número i o unidad imaginaria, definido como: i = (0 , 1 )